Wave Problem Set
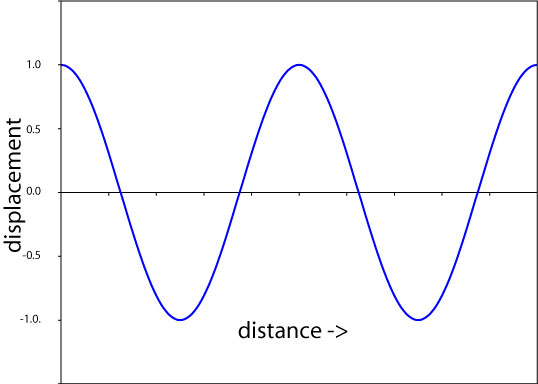
1) In the image above, indicate where the phase of the wave is 0, pi/4, pi/2, 3pi/4, pi, 3pi/2, and 2pi.
If the wavelength is 25 meters, what is the phase at 37.5 meters?
On the figure, sketch a wave that has twice the wavelength, half the amplitude and is directly out of phase at X=0 (X is distance) relative to the wave indicated.
Use a spreadsheet for problems 2-4 below. Enter generalizable equations for
waves on two worksheets and put the sum on a third worksheet. This will allow you to easily change various parameters and quickly visualize the result.
Email your spreadsheet to the instructor when you hand in this assignment. Put your name, the course number and "waves" in the subject line of the email.
2) For the following wave,
phase = 0 at x = 0 angstroms,
wavelength = 3 angstroms
amplitude = 10 (arbitrary units)
Graph of the displacement from 0 to 10 angstroms, at 0.1 angstrom increments.
3) For the following wave,
phase = pi/2 at x = 0,
wavelength = 3 angstrom
amplitude = 10
Graph of the displacement at 0.1 angstrom increments, from 0 to 10 angstroms.
4) Add the wave in problem #2 to the wave in problem #3 by summing the displacements at each distance.
Plot the resulting wave.
5) Consider the three waves a,b,c
a) phase = 0 at x = 0,
wavelength = 3 angstroms
amplitude = 5
b)
phase = pi/2 at x = 0,
wavelength = 3 angstroms
amplitude = 5
c)
phase = pi at x = 0,
wavelength = 3 angstroms
amplitude = 5
i) Add wave a to wave b. What are the phase, wavelength and amplitude for the resulting wave? Write out the equation for displacement vs distance.
ii) Add wave a to wave c. What are the phase, wavelength and amplitude for the resulting wave?
sample spreadsheet
